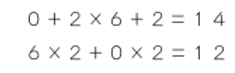保護者の方へ
試行力問題を解く目的は，カリキュラム学習のように理論体系を構築していくことにはありません。あえて言えば，試行力問題は解けても解けなくてもどちらでもよいのです。子どもが悪戦苦闘しながら頭をフル回転させることで，考える力を鍛えることが目的です。
よって，以下の２点は厳守してください。
解けるようになることは目的ではないのですから，教える必要はありません。どうしても手が進まないときに少しだけ助言をする程度にとどめてください。そのときのその子にとって解けない問題は，どうやっても解けませんし，それはなんら気にすべきことではありません。
気が向かないときに頭をフル回転させられる人間はいません。
教えない
無理やり解かせない
数の性質
開成中・武蔵中で以前に出題された，その場で記数法を示して考えさせるタイプの問題です。それらと 比べてもかなり試行錯誤の量が多くなっていますが，低学年から高学年まで，誰にとっても正解可能な難問になっています。
２年生でも解けますが，小６上位生でも正解しにくい問題です。
与えられた式が成り立つように，Ａ～Ｊに０～９を入れる問題です。
与えられた式が成り立つように，Ａ～Ｊに０～９を入れる問題です。
２と５，６と９のカードの回転・裏返しOKで２０２６を並びかえた４桁の整数について計算をする問題です。
２と５，６と９のカードの回転・裏返しOKで２０２６を並びかえた４桁の整数について計算をする問題です。
数字カードを並べかえてできる整数の差に関する問題です。
数字カードを並べかえてできる整数の差に関する問題です。
数字カードを並べかえてできる整数の差に関する問題です。
大小関係のある和分解の問題です。こちらは云わば基本編で，応用編もあります。
表の位置による大小関係のある和分解の問題です。
表の位置による大小関係のある和分解の問題です。
右下に進むにつれて大きくなる数がならぶ表において２つの和分解を組みあわせた問題です。…低学年でも解けくことができますが，女子学院や慶應普通部模試で出題するとかなりの低正答率になるくらいには難しいと思います。
和分解をしつつ，数を三角形状に並べる問題です。
和分解をしつつ，数を三角形状に並べる問題です。
和分解をしつつ，数を三角形状に並べる問題です。
和分解をしつつ，数を三角形状に並べる問題です。
和分解をしつつ，数を三角形状に並べる問題です。
和分解をしつつ，数を三角形状に並べる問題です。
和分解をしつつ，数を三角形状に並べる問題の応用編です。
三角形状の数表に並ぶ数を区切って２けたの整数を作り，その和について考える問題です。
各順位の最高点と最低点を考える問題です。
各順位の最高点と最低点を考える問題の第２弾です。
各順位の最高点と最低点を考える問題の第３弾です。
ひっ算の虫食い算について，各位置に入る最小の数と最大の数を求める問題です。
２０２１の小町算です。
２，０，２，３の間に＋－×÷（）を入れて式を作る問題です。
２，０，２，３の間に＋－×÷（）を入れて式を作る問題です。
20252025という数字のならびの式の答えを2025にする問題です。
２・０・２・６を並びかえて，答えが１から１０までの整数になる式を作る問題です。
一の位が等しいいくつかの整数の和の下２桁に関する問題です。
一の位が等しいいくつかの整数の和の下２桁に関する問題
の第２段です。
一の位が等しいいくつかの整数の和の下２桁に関する問題
の第３段です。
一の位が等しいいくつかの整数の和の下２桁に関する問題
の第４段です。
マス目の数でかけ算の分配法則を表し，かけ算九九と2025の関係に気づかせる問題です。
右と下のマスほど数が大きくなるようにマス目に数を入れる問題に，和分解の要素を入れています。
右と下のマスほど数が大きくなるようにマス目に数を入れる問題に，和分解の要素を入れています。
右と下のマスほど数が大きくなるようにマス目に数を入れる問題に，和分解の要素を入れています。
右と下のマスほど数が大きくなるようにマス目に数を入れる問題に，和分解の要素を入れています。
右と下のマスほど数が大きくなるようにマス目に数を入れる問題に，和分解の要素を入れています。
１グラムのおもりは１個，２グラムは２個…という規則で天秤のつりあいを考える問題です。
条件付きの順位・和分解の問題です。投票の問題として出題されることが一般的です。
順位・和分解と推理の問題です。
よくある，デジタル数字の問題です。
デジタル数字を作るのに使うマッチ棒の本数と，表すことができる整数に関する問題です。
マッチ棒でデジタル数字を作る問題の第３弾です。
マッチ棒でデジタル数字を作る問題の第４弾です。
マッチ棒でデジタル数字を作る問題の第５弾です。
デジタル数字の問題を，数式に絡めました。
整数を２個の整数の積に分解していく問題です。
整数を２個の整数の積に分解していく問題です。
整数を２個の整数の積に分解していく問題の第３段です。
整数を２個の整数の積に分解していく問題の第３段です。
２０２４のとなりあう位の数の差はすべて２です。このような数について調べていく問題です。
各位の数の並びかえと，となりあう数の和と差に関する問題です。
2023のように，３種類の数字が使われている年号を考える問題です。
約束記号と整数の割り算の問題です。
数と調べ上げの，コンパクトな問題ですが，少し条件を緩めたり付け加えたりすると，一挙に最難関中レベルの問題になります。
和と積の値に関する試行力問題，一発で正解できるでしょうか。
５つの整数の和と積の大小関係に関する問題です。
各位の数の和が７となる整数（年号）の問題です。
カードに書かれた数をきまりにしたがって計算する問題です。かなり慎重に調べることが必要です。
選んだカードに書かれた数をきまりにしたがって計算したときの答えについての問題です。論理的に積み上げる発想が必要となります。
マスに和が等しくなるように，マス目を分割する問題です。
マスに和が等しくなるように，マス目を分割する問題の第２弾です。
奇数と偶数の性質に着目して解く虫食い算です。
数字の組合せを場合分けて考える問題です。
式に現れる数字の個数について，場合分けを行います。
式に現れる数字の個数について，場合分けを行います。
式に現れる数字の個数についての場合分けと調べ上げの問題です。
式に現れる数字の個数について場合分けを行って考えるシリーズです。
式と数字の個数・ひき算２
２０２０１月１日以降の年月日についての，パズル・調べ上げ問題です。
２０２０１月１日以降の年月日についての，パズル・調べ上げ問題です。
２０２０を並べた数列の１か所に＋を入れた答えについて考える問題です。
343010に現れる２つの３は，それより下の位にある３より小さい数が３個になっています。このような性質をもつ数についての，調べ上げの問題です。
各位に９より大きい数を書くことを許して，‘２０２０’を並びかえてみます。
2020年の洛南中で出題された数表の仕組みを使って試行力問題を作りました。
等間隔で分割した円を重ねて見る問題です。
等間隔に点を打った円を重ねる問題の第２弾です。
いくつかの整数を，連続する整数へ和分解する問題です。
整数を連続する整数の和に分解していく問題の第２弾です。
２けたの整数の各位の数の和と積の差に関する問題です。
２けたの整数の各位の数の和と積の差に関する問題の第２弾です。
２進法の仕組みを利用したシンプルな数のパズル問題です。
平面図形
指定された位置に頂点を持つ六角形を探す問題です。
６つの辺の長さが等しい「六等辺六角形」の探し方についてマス目の上で考える問題です。
６つの辺の長さが等しい「六等辺六角形」の探し方についてマス目の上で考える問題です。
６つの辺の長さが等しい「六等辺六角形」の探し方についてマス目の上で考える問題です。
マス目を，いくつかの点に近い部分で分割する問題です。
点を結んで，空間をできるだけ多くの領域に分割する問題です。
点を結んで，空間をできるだけ多くの領域に分割する問題です。
点を結んで，空間をできるだけ多くの領域に分割する問題です。
正方形の辺および内部にある点の個数に関する問題です。
正方形の辺および内部にある点の個数に関する問題です。
正方形の辺および内部にある点の個数に関する問題です。
正方形の辺および内部にある点の個数に関する問題です。
方眼紙を折り重ねていく問題です。
進行方向と左右の空間感覚が問われる問題。かなりすっきりとしています。
進んできた経路と奇数と偶数によって進む方向が決まるスゴロクの問題です。
麻布的な，正六角形のマス目移動の問題です。
正方形を組み合わせた図形の周の長さに関するパズル問題です。図形に関する場合分けと調べ上げ力を培いたい最難関受験生にもお勧めです。
長方形から小正方形をいくつか取り除いたときの周りの長さに関する問題です。
長方形から小正方形をいくつか取り除いたときの周りの長さに関する問題です。
針金を曲げてできる形についての調べ上げの問題です。自然数の和分解が鍵となります。
長方形の紙をはさみで切り分けたときの周の長さの和を求める問題です。
長方形の紙をはさみで切り分けたときの周の長さの和を求める問題です。
正三角形と正六角形の長さについてのパズル問題です。
正方形のマス目を３つの部分に分割する問題です。
正方形を分割するパズルの第２弾です。
正方形を分割するパズルの第３弾です。
紙をななめに切って正方形を組み立てる問題です。
マス目に穴をあけてから切って組み立てなおす問題です。
マス目に穴をあけてから切って組み立てなおす問題です。
マス目に穴をあけてから切って組み立てなおす問題です。
ななめにつながるようにマスを選んでいく問題です。
ななめにつながるマスをあしらったグッズを販売しています。
ななめにつながるようにマスを選んでいく問題です。
２枚のカードを組みあわせて囲いをつくる問題です。
２枚のカードを組みあわせて囲いをつくる問題です。
複数の長方形を切って組みなおす問題です。
ピース並べ・１
ピースを並べて形を作る問題です。
ピースを並べて形を作る問題です。
図形と場合の数の問題です。
となりあうマスに置いたご石を取り去る問題です。図形の対称性を利用しながら調べ上げます。
となりあうマスに置いたご石を取り去る問題の第３弾です。図形の対称性を利用しながら調べ上げます。
となりあうマスに置いたご石を取り去る問題の第４弾です。図形の対称性を利用しながら調べ上げます。
碁盤（ごばん）においてコマが移動する問題です。麻布，駒場東邦，栄光学園，キッズBEE等に向いています。
マス目上を動く２つのコマの重なりについての問題です。
図形の回転移動と場合分け・調べ上げの融合問題です。もちろん3.14は使いません。
正三角形を組み合わせたコースを移動する２つのコマの間の距離を考える問題です。
カードを並びかえて長方形を作る問題です。かなりハードです。
デジタル数字の２，０は点対称です。
階段状の折り紙の問題です。
ねんどと竹ひごによって，２０２０をいろいろな向きで組み合わせる問題です。
ねんどと竹ひごによって，２０２０をいろいろな向きで組み合わせる問題の第２弾です。
大きさの異なる円の動きについて考える問題です。3.14等は使いません。
開成中・平成７年の，２本の直線の線対称の問題を，試行力向けに展開してみました。
正多角形を対角線によっていろいろな多角形に分割する問題です。
正三角形のカードとカードの間の道のりについて考える問題です。
正三角形のカードとカードの間の道のりについて考える問題の第2弾です。
正方形と直角二等辺三角形の個数について考える問題です。
３本の直線を対称の軸とした線対称形について，いろいろと図を描く問題です。
８の字に組み合わせた円と棒を光らせる問題です。
８の字に組み合わせた円と棒を光らせる問題の第２弾です。
棒を使って正多角形の組を色々と作る問題です。
棒を使って正多角形の組を色々と作る問題です。
棒を使って正多角形の組を色々と作る問題です。
立体図形
立方体の５つの頂点を結んで多面体を作る問題です。
見取り図から展開図への切り開きと，展開図から見取り図への組み立てを行う問題です。栄光やフェリスの受験者にもおすすめです。
２つの積み木を組みあわせて色々な立体を作る問題です。
２つの積み木をあしらったグッズを販売しています。
２つの積み木を組みあわせて色々な立体を作る問題です。
２つの積み木を組みあわせて色々な立体を作る問題です。
２つの積み木を組みあわせて色々な立体を作る問題です。
２つの積み木を組みあわせて色々な立体を作る問題です。
立方体を組み合わせた立体の外から見える面の個数に関するパズル問題です。立体の形を考える力を培いたい最難関受験生にもお勧めです。
立方体の積み木を組み合わせた立体の表面積や見え方に関する問題です。
頂点の重なりの条件にしたがって展開図を完成させる問題です。
頂点の重なりの条件にしたがって展開図を完成させる問題の第２弾です。
何種類の積み木が見えるか，という投影の問題です。
さいころの目の向きを考えにいれて数字が連続するように並べる問題です。
正四面体の展開図を切り取る問題です。
矢印の向きにさいころを回転させる問題です。
さいころの上の面の目の分だけさいころを自由に転がす問題です。
場合の数・論理
キッズBEE第９回ファイナルの「もんだい９」に触発されて作りました。いろいろなケースを考えながら，作業をしていく力が求められます。「最難関問題」に同タイプの問題があります。
紙テープの折り重ね方に関する問題。初見問題に手を使って切り込むことが求められます。「最難関問題」に姉妹問題あり。
横に長い紙を折り込んでいく問題です。
調べ上げればサッと解ける問題です。
数字カードで日付けを作る問題です。
カードを組みあわせて日付けを作れるだけ作る問題です。
カードを組みあわせて日付けを作れるだけ作る問題です。
特定の数字を含む数が書かれたカードを順に取っていく問題です。
特定の数字を含む数が書かれたカードを順に取っていく問題です。
特定の数字を含む数が書かれたカードを順に取っていく問題です。
特定の数字を含む数が書かれたカードを順に取っていく問題です
８枚のカードで坊主めくりをする問題です。低学年でも解ける試行力タイプの問題ですが，難易度は開成レベルになってしまいました。開成・栄光学園・渋谷幕張を受験する６年生にも
おすすめ？です。
８枚のカードで坊主めくりをする問題の第２弾です。
８枚のカードで坊主めくりをする問題の第３段です。
８枚のカードで坊主めくりをする問題の第４段です。
和が定められた数になるように交代でカードを取っていくゲームにおいて必勝パターンを探す問題です。
和が定められた数になるように交代でカードを取っていくゲームにおいて必勝パターンを探す問題です。
和が定められた数になるように交代でカードを取っていくゲームにおいて必勝パターンを探す問題です。
あいこの得点を「ストック」しておけるじゃんけんゲームの問題です。近頃の開成にありがちな，「がんばって場合分けよう」というタイプの問題です。
コマを動かして陣地をつくる問題で，積分解や和分解の複合問題です。
コマを動かして陣地をつくる問題で，積分解や和分解の複合問題です。
コマを動かして陣地をつくる問題で，積分解や和分解の複合問題です。
コマを動かして陣地をつくる問題で，積分解や和分解の
複合問題です。
コマを動かして陣地をつくる問題で，積分解や和分解の複合問題です。
３つのコマを動かして，定められた配置にする問題です。
ゴールまでの最短経路を探す問題です。行き当たりばったりではうまく解けません。
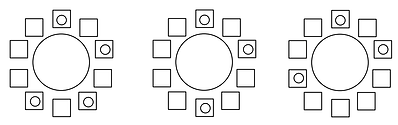
マス目における，椅子の配置に関する問題です。
女子学院のマス目に数字を入れるパズルを１次元とすると，その２次元版の問題です。それぞれの数字が何個まで入れられるかを検証する必要があります。
女子学院のマス目に数字を入れるパズルを１次元とすると，その２次元版の問題です。それぞれの数字が何個まで入れられるかを検証する必要があります。
マスの間の距離を表すように数字をマス目に入れる問題です。
マスの間の距離を表すように数字をマス目に入れるパズルの第２弾です。
マスの間の距離を表すように数字をマス目に入れるパズルの
第３弾です。
マスの間の距離を表すように数字をマス目に入れるパズルの第４弾です。
数字の枠の組みあわせを考える問題です。女子学院のマス目に数字を入れるパズルを１次元とすると，その２次元版の問題です。
マス目を加えることでコマの動く範囲がどのように変化するのかを考える問題です。
通行不能なマスを置くことで，コマの動く範囲がどのように変化するのかを調べていく問題です。
マス目の上で点と点の間の道のりの条件を満たすように新しい点を打っていく問題です。
マス目の上で点と点の間の道のりの条件を満たすように新しい点を打っていく問題です。
マス目の上で点と点の間の道のりの条件を満たすように新しい点を打っていく問題の第３弾です。
マス目の上で点と点の間の道のりの条件を満たすように新しい点を打っていく問題の第４弾です
マス目の上で点と点の間の道のりの条件を満たすように新しい点を打っていく問題の第５弾です。
となりあうマスの○の有無に応じてマスが相互作用で変化していく，コンウェイのライフゲームの問題です。
となりあうマスの○の有無に応じてマスが相互作用で変化していく，コンウェイのライフゲームの問題です。
○の有無をいれかえ続けて，すべての○を消すパズルです。
○の有無をいれかえ続けて，すべての○を消すパズルです。
○の有無をいれかえ続けて，すべての○を消すパズルです。
○の有無をいれかえ続けて，すべての○を消すパズルです。
○の有無をいれかえ続けて，すべての○を消すパズルです。
○の有無をいれかえ続けて，すべての○を消すパズルです。
上下左右にとなりあう数を入れないようにしたマス目を組みあわせる問題です。
数字のコマが移動できなくなるまでの最短数を考える問題です。
カードを用いて時刻をあらわす，場合分けの問題です。
正三角形のマス目に重複なしで数字を入れる問題です。
正三角形のマス目に重複なしで数字を入れる問題です。
正三角形のマス目に重複なしで数字を入れる問題です。
正三角形のマス目に重複なしで数字を入れる問題です。
３つの輪の重なりにおいて，整数の和と差に注目をした調べ上げを行う問題です。
数字を割り当てた輪を色々な仕方で重ねる問題です。
数字を割り当てた輪を色々な仕方で重ねるパズルの第２弾です。
数字を割り当てた輪を色々な仕方で重ねるパズルの第３弾です。
数字を割り当てた輪を色々な仕方で重ねるパズルの第４弾です。
じゃんけんの問題と勝敗の問題を絡めてみたところ，面白いことになりました。
トーナメントの問題では，試合数は参加人数－１となりますが，それとは別に数量的に扱える事柄を考えてみた問題です。
差が縮まる・広がる，追いこす・追いこさないといったことを考える推理の問題です。
最難関問題「速さと比のパズル」から速さの計算と比の要素を除いた問題です。
攪乱順列＋αの条件下で調べ上げていく問題です。
推理と計算を合わせた問題です。
年令について場合分けて答えを探す問題です。
和分解と積分解を組み合わせた調べ上げの問題です。
さいころを１０個振ったときの，２つずつの目の和について考える問題です。
調べ上げ（和分解）と推理の融合問題です。
２人のコマが押しあいをするスゴロクの問題です。
２のマスにとまると２つ進む，２０２０を並べたすごろくの問題です。
コマが往復したり向きを選んだりするすごろくの問題です。
コマが往復したり向きを選んだりするすごろくの問題です。
コマが往復したり向きを選んだりするすごろくの問題です。
コマがマスに書かれた数字のぶんだけ左右に進む，パズル問題です。
マスに書かれた数字のぶんだけコマが左右に往復する問題の第２弾です。
今年（2023年）の開成の点移動の問題を，２つのコマの直線上の設定に変えたものです。
２０面ダイスの出た目をストックできるすごろくの問題です。
一筆書きならぬ，２，３，４筆書きの問題です。
二筆以上，最小の画数を求める問題です。
周回可能なルートを作るために道を追加する問題です。
周回可能なルートを作るために道を追加する問題です。
周回可能なルートを作るために道を追加する問題です。
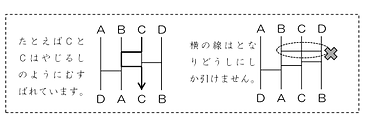
あみだくじを作る問題です。
あみだくじを作る問題です。
あみだくじを作る問題です。
あみだくじを作る問題です。
あみだくじを作る問題です。
あみだくじを作る問題です。
デジタル数字の２０２０を並べた道順についての問題です。
同じ道と頂点を２度通過しないという条件下で遠回りの道もふくめて道順を調べ上げる問題です。
色々な遠回りの道順を考える問題です。
遠回り＆同じ交差点の複数回通過が可能な，道順の問題です。
遠回り＆同じ交差点の複数回通過が可能な，道順の問題の第２弾です。
遠回り＆同じ交差点の複数回通過が可能な，道順の問題の第３弾です。
遠回り＆同じ交差点の複数回通過が可能な，道順の問題の第４弾です。
遠回り＆同じ交差点の複数回通過が可能な，道順の問題の第４弾です。
マス目上の点をできるだけ短い経路で結ぶ方法が何通りあるかを考える問題です。
マス目上の点をできるだけ短い経路で結ぶ方法が何通りあるかを考える問題の第２弾です。
マス目上の点をできるだけ短い経路で結ぶ方法が何通りあるかを考える問題の第３弾です。
マス目上の点をできるだけ短い経路で結ぶ方法が何通りあるかを考える問題の第４弾です。
マス目上の点をできるだけ短い経路で結ぶ方法が何通りあるかを考える問題の第５弾です。
栄光学園2018や洛南中2018のような，最短距離ではない道順に関する問題です。
栄光学園2018や洛南中2018のような，最短距離ではない道順に関する問題の第２弾です。
すべての部屋を通過できないようにじゃまをする問題です。
２本の最短ルートに囲まれた部分に関する問題です。
２本の最短ルートに囲まれた部分に関する問題です。
２本の最短ルートに囲まれた部分に関する問題です。
円順列タイプの試行力問題です。
円順列タイプの試行力問題です。
回転対称性について考える，図形の場合の数の問題です。
デジタル数字のカードを回転させて並べかえる問題です。
透明な数字のカードを裏返す問題です。
階段状にカードを並びかえる問題の，試行力版です。
カードを大きい順にならびかえる問題です。
カードを大きい順にならびかえる問題の第２弾です。
カードを大きい順にならびかえる問題の第３弾です。
カードを大きい順にならびかえる問題の第４弾です。
カードを大きい順にならびかえる問題の第５弾です。
コインの 裏返し方と並び順についてのパズル問題です。
コインの裏返しと並び方に関する問題の第２弾で す。
コインの裏返し方と並び順に関する問題の第３弾です。
コインの裏返しと並び順に関する問 題の第４弾です。
表裏に異なる数字が刻んであるコインを裏返していく問題です。
表裏に異なる数字が刻んであるコインを裏返していく
問題の第２弾です。
表裏に異なる数字が刻んであるコインを裏返していく問題の第３弾（試行力版）です。
かく乱順列を並べかえていく問題です。
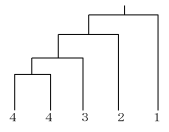
樹形図でていねいに調べ上げていきます。
かく乱順列を並べかえていく問題です。
樹形図でていねいに調べ上げていきます。
かく乱順列を並べかえていく問題です。
樹形図でていねいに調べ上げていきます。
○△が並んだ列に操作を繰り返す問題です。
○△が並んだ列に操作を繰り返す問題です。
コインの投げによって次に並ぶ数のきまりが変わる問題です。
コインの投げによって次に並ぶ数のきまりが変わる問題です。
調べ上げつつ，仕組みを見つける並べ方の問題です。
和分解において，同じ数が現れる回数の制限を扱った問題です。
正多角形のすべての頂点に１回ずつ重なる方法についての問題です。
奇数・偶数の並び順に関する推理の問題です。
４けたの整数の各位の数を並びかえ，となりあう数の奇偶を考える問題です。
解が一定の範囲をとる，不定方程式の調べ上げ問題です。
金額の組み合わせの和や差について考える，調べ上げタイプの問 題です。
２０２０を並びかえてできる魔方陣の問題です。
魔方陣の重ねあわせを通して，可能な数の配置について考えていく問題です。
三角形の魔方陣を重ね合わせる問題です。
やや変則的な魔方陣の問題です。
カードに書かれた数字がカードとカードの間の道のりを表している問題です。
カードに書かれた数字がカードとカードの間の道のりを表している問題の第２弾です。
カードに書かれた数字がカードとカードの間の道のりを表している問題の第３弾です。
数と記号の並び方を変える約束記号の問題です。
ご石を並べてから取り除く問題です。
記号の置き換え操作に関する問題です。
５人のうち１人が２回出場して３対３のチーム戦を行う問題です。
三角形のタイルを並べていろいろな長さにする問題です。
三角形のタイルをならべる，調べ上げの問題です。
和が等しくなるようにカードを交換する推理の問題です。
渋滞に関する問題の試行力版，第一弾です。速さではなく操作の回数で考えます。
渋滞の問題の第２弾で，渋滞区間が拡大していく問題です。試行力問題として，速さの代わりに操作の回数で考えます。
いくつかの条件から，誕生日を推理する問題です。
となりあう数の差についての条件を満たす整数の個数を樹形図などで整理する問題です。
さいころの目に応じて進んでいく，道順の問題です。
階段状のマス目をすきな向きで重ねあわせる問題です。
カードに書かれた数に関する推理の問題の低学年版です。
引いたカードに書かれた数についての推理の問題の第２弾です。
規則性
正三角形のカードに３個の数字を書いた問題です。単元的には図形と規則性の融合問題ということになります。
カードを規則にしたがって並び替える問題です。
よくある，規則に従った動きに関する調べ上げと規則性の問題です。
周期性に関するやや面倒な問題です。
植木の本数と「閉じた区間」に関する問題です。
サイズの異なる箱に，カードを順番に入れていく問題です。
前の２つの数の積が次の数になるという数列を割ったときの余りに関する問題です。
フィボナッチ数列と剰余に関する問題です。
等比数列と剰余に関する問題です。
たし算とかけ算によって規則的に並んだ数を，別の数で割ったときの余りについて考える問題です。
カレンダーの各週から日にちを１つずつ選んで和と差を考える問題の試行力版です。
１２か月分をつなげたカレンダーにおいて，図のような枠で日付を囲む問題の，試行力版です。
３個の整数が書かれたカードを並べてできる数表に関する問題の試行力版です。
一の位と十の位の数を，きまりにしたがって繰り返し操作することに関する問題です。
文章題
日数，剰余に関する，６年生にとっても解きにくいタイプの問題です。
２人が同じ舟や別々の舟に乗って，すべての舟を対岸に運ぶ問題です。
２人が同じ舟や別々の舟に乗って，すべての舟を対岸に運ぶ問題です。
