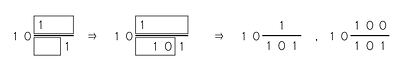作図
箱の内側や外側において,ひもの届く範囲を作図する問題です。コンパスを使用します。
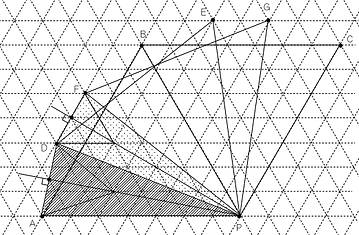
正八四面体の各頂点からの近さ・遠さの範囲を考える問題です。定規とコンパスを用いた作図の設問を伴っています。
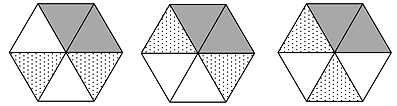
正三角形のマス目を利用して外接円を作図したり,面積を求めたりする問題です。
正三角形のマス目を利用して外接円を作図したり,面積を求めたりする問題です。
正三角形を敷き詰めた平面において長方形を直定規1本で作図する問題です。
正三角形のマス目上で正三角形を作図する問題です。
正九角形を利用して,直定規のみを用いて色々な正三角形を作図する問題です。
正九角形の内部に,いろいろな大きさの正三角形を作図する問題です。三角定規を使用します。
面積の大小に関する条件を満たす頂点の位置を定規とコンパスで作図する問題です。
面積の大小に関する条件を満たす点の範囲を,三角定規を使用して作図する問題です。
面積の大小に関する条件を満たす頂点の位置を定規とコンパスで作図する問題です。
図形の面積の関係を満たす頂点の範囲をコンパスなどを使って作図する問題です。
速さ
水位が上がるにつれて給水管からの距離は短くなっていく…,では,水はどう増えていくのか,という問題についての思考実験です。
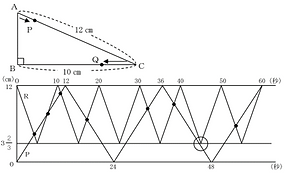
速さと図形の複合問題です。エディアカラ紀(6億年ほど前)のネミアナ・シンプレックスの化石を見て思いつきましたが,ネミアナの生態学的構造と問題の作りは特に関係ありません。なお,この問題ではやや特殊な比の使い方をします。この扱い方にクローズアップした問題が,「逆比の双対性」です。
すれ違いにかかる時間の差についての問題です。
平行ではない方向に移動する2点のシャドウを考える問題です。
開成中2016のように,傾斜によって速さが変化する問題です。
開成中2016のように,傾斜によって速さが変化する問題です。
すべり台の下から上に向けて箱を滑らせる問題です。
列車の長さが長くなるほど速さが遅くなることによって,距離と速さがリンクしている問題です。
渋滞に関する問題です。第一弾はシンプルに,渋滞区間の大きさが変わらない設定になっています。
渋滞の問題の第2弾で,渋滞区間が拡大していく問題です。
渋滞の問題に,ニュートン算と通過算を絡めています。
円周上を移動する複数の点が重なる位置を結ぶと星形になる問題です。
円周上の点移動によってつくられる図形の問題です。
列車の中で往復するボールどうしの旅人算です。
列車の長さ=車両の長さ×車両数という条件から,答えを絞りこむ問題です。
車両数と速さが反比例する鉄道模型の問題です。
車両数と速さが反比例する鉄道模型の問題の第2弾です。
車両数と速さが反比例する鉄道模型の問題の第3弾です。
細かい状況整理をしっかり行う通過算です。
点移動を特定の方向から見たときに成り立つことを考える問題です。
差が縮まる・広がる,追いこす・追いこさないといったことを考える推理の問題です。
試行力問題「速さのパズル」に速さと比の要素を加えた問題です。
足の動く速さを変えることと動く歩道をからめた,歩数と歩幅の問題です。
歩数と歩幅の応用問題です。
速さの和と差を利用する旅人算の問題です。
加速していくラジコンカーによる,追いつきの旅人算の問題です。
直角三角形上の点移動と射影の問題を��グラフで考えます。
移動しながら膨張していく円によって,時間とともに距離が大きくなる問題です。
円が移動しながら加速膨張していく問題です。
単位時間あたりに変化する面積の値のグラフの問題です。
速度変化のグラフの面積版です。
信号による停止と到着時刻の範囲を考える問題です。
速さ・規則性・数の性質を合わせて考える問題です。
旅人算の応用問題で,すれ違いが特定の地点でしか�行えない問設定にしています。
速さと規則性の複合である,列車のダイヤに関する問題です。
車輪と速さの応用問題で,数の性質に関する発��想も求められます。
時針・分針・秒針の位置関係について時計に等分割した目盛りを入れて考える問題です。2020年栄光学園の類題と言っていい問題です。また,この発想は以前に単元研究の「時計算と周期」である程度まとめています。
時針・分針・秒針が等間隔に並ぶ可能性について考えていく問題です。
一定の速度で動く針Bの差す目盛りによって針Aの速さが変わる問題です。
時針・分針・秒針の間の角度の成立・不成立を考える問題です。
正三角形を組みあわせたマス目の辺上を移動する2点間の道のりについて考える問題です。
組みあわせた車輪がそれぞれ回転する速さの問題で,流水算や動く歩道の問題と同種です。
流水算・歩数の問題を融合した,車輪同士の組みあわせの問題です。
流水算・歩数の問題を融合した,車輪同士の組みあわせの問題です。
針が加速するタイマーに目盛りを入れたりする問題です。
流速が加速していく川の流水算です。
ラジコンカーの形によって,風速の影響が変わってくる問題です。
車体の形によって風速の影響が変わる速さの問題です。
点移動のシャドウの動きを追っていく(だけの)問題です。
シャドウの動きをしっかり追っていく問題です。
規則性
複雑な図形について何筆でかくことができるかを求める問題です。
周回可能なルートを作るために道を追加する問題です。
1年を365.2425日とした場合に,グレゴリオ暦とは異なる暦を作ってみよう,という問題です。
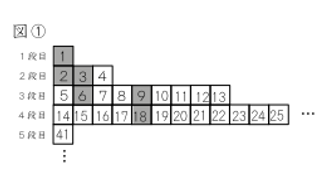
見るからに麻布・栄光学園的な重ね合わせの問題ですが,数表のセンスで解くように誘導を入れています。
3で割った余りを並べた数列における線対称な部分の配置を考える問題です。
三角形型の数表における,任意の整数の倍数の配置に関する問題です。説明を求めるタイプの設問になっています。
正三角形のマス目において,直線の本数と交点の個数の関係を考える問題です。
2種類の線を重ねていくときにできる領域の数に関する問題です。
下の図は4本の線分から成る4辺形です。このようなN辺形の頂点についての問題です。
調和数列を紹介し,その性質を考えていく問題です。
フィボナッチ数列を真正面から扱った問題です。
いろいろなフィボナッチタイプの数列のn番目の数に関する問題です。
以下のように,連続する2つのフィボナッチ数の平方数の和がフィボナッチ数であることを説明する問題です。
連続するフィボナッチ数の平方数の和についての問題です。
となりあうフィボナッチ数の積の和を求める問題です。
文字列がフィボナッチ数列的につなげられていく数列の問題です。
以下のきまりにしたがったあらゆる数列において,どのような整数が現れるのかを考える問題です。
トリボナッチ数列の性質を正面から考える問題です。
2でちょうど2回割り切れるフィボナッチ数は存在しないことを説明せよ,という問題です。
フィボナッチ系統の数列,テトラボナッチ数列について2つの考え方を探っていく問題です。
フィボナッチ式に並ぶ整数の大小関係に注目して,別の構造を見出していく問題です。
フィボナッチ数列に関する正統的なアプローチを重視した問題です。
やや複雑な和と差の規則をもつフィボナッチ数列の問題です。
フィボナッチ数列系の問題の第3弾です。「くり上がり」「くり下がり」について考えます。
塗り分けの場合に数について,等差数列・等比数列・フィボナッチ数列・変則的フィボナッチ数列等が現れてくる問題です。
規則を複数のフィボナッチ数列に分析し,その後組みあわせて考える問題です。
動く点が図形の頂点を移動する道順に関する問題です。フィボナッチ系の発想に収束します。
点が頂点を移動する方法の場合の数をフィボナッチ数列的にとらえる問題です。
さいころを同じ目の面を合わせて段段に並べたときに,上の面がぞろ目になる確率に関する問題です。
道順の応用問題です。法則性,数の性質まで考えます。
マス目の塗り分けにおいて成立する法則を求める問題です。
正方形をらせん状に敷きつめて,辺の長さがフィボナッチ数になる様子を表したグッズを作成しました。
フィボナッチ螺旋上を点が移動する問題です。
フィボナッチ螺旋上を点が移動する問題です。
フィボナッチ数の平方数の和などに関する問題です。
2つのフィボナッチ数列をかけあわせる問題です。
フィボナッチ数列になりきらない規則性を考える問題です。
となりあう位の数の差についての条件を満たす整数の個数を考える問題です。フィボナッチタイプの数列を利用します。
記号列を規則に従って生成していく問題です。
数列と剰余に関する問題です。
小数の等差数列に対して,整数部分の数列と概数の数列を比べる問題です。
コインをいろいろな仕方で裏返したときのコインの順番に関する,規則性の問題です。
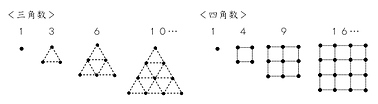
三角数や四角数に基づく数表の問題はよく見かけますが、この問題は対数の仕組みに基づいています。
各段に3の累乗数の個数の整数を並べた数表の問題です。
2024で割った剰余では扱いに困る…,それでは,という問題です。
連続する整数の組みと,剰余に関する条件を考える問題です。
整数を3で割った余りを順に四角形に並べていく数表の規則性に関する問題です。
四角数(平方数)のよくある数表を変則的にした問題です。
よくあるらせん型の数表において3の倍数がとなりあう場所について考察する問題です。
自然数をらせん状に並べていく数表と,斜めに傾けた正方形の関係を扱う問題です。
6つの辺の長さが等しい「六等辺六角形」の探し方についてマス目の上で考える問題です。
らせん状に整数を並べた数表の一部分に注目をして,そこで成り立つ事柄などを考える問題です。
平方数表の一部を切り抜いた三角数表状の数表の問題です。
2の累乗数で区切った三角数表に関する問題です。
左端が2の累乗数である数表に関する問題です。
正三角形のマス目における数表の問題です。
正三角形の方眼上に螺旋状に数を並べた数表の問題です。
正三角形を並べた表において螺旋状に整数を並べた表に関する問題です。
四角数の数表において,たて横2マスの枠で囲った数の和が等しくなる箇所を求める問題です。
3個の整数が書かれたカードを並べてできる数表に関する問題です。
三角数の数表においてマス目を囲う問題です。少し古い開成や筑駒のような感じですね。
かけ算九九の表を数表に見立てて,並んでいる積の間の法則性を考える問題です。
正方形と正八角形をしきつめた数表の問題です。明白な対称性が生じるように設定しています。
分母が2020,分子が三角数である分数列の問題です。
各位の数について特定の条件を満たす整数の個数と規則性の問題です。
いろいろな多角数について,となりあう数の和を考える問題です。
三角数の数列と,7の倍数の数列を比べる問題です。
正六角形内の正三角形の個数についての問題です。
図形を「類似した形」で成長させていく問題です。
図形を「類似した形」で成長させていく問題です。
正六角形・正方形・正三角形のタイルをきまりにしたがって敷きつめていく問題です。
図のような模様で平面を埋め尽くす問題です。
多角形の頂点及び内部の点を結んで,できるだけ多くの領域に分割する,図形と規則性の問題です。
点と点を交差しない線分で結んでいったときに,平面を最大で何分割できるのかを考える問題です。
周のマス目の数が決まっている長方形の組みあわせを考える,平面図形と規則性の問題です。女子学院のマス目に数字を入れるパズルを1次元とすると,その2次元版の問題です。
移動する正三角形の辺上を移動する点の軌跡に関する問題です。麻布的な図形と規則性の問題です。
三角形を重ね合わせたときに辺に囲まれた部分が何個できるかを考える問題です。
三角形と四角形を重ね合わせてできる区域の個数に関する問題です。
等間隔に並ぶ点をできるだけ少ない個数消して,正方形を作れなくする問題です。
三角形の内部に調和数列が現れる問題です。
カードを裏返してシャッフルする問題です。
ある整数÷nと,÷(n+1)の剰余を比べる問題です。
積み木を塗り分ける場合の数の問題で,規則性を見出して解くことを意図しています。
ルーローの三角形を,敢えて平行移動させてみる問題です。
場合の数・論理
キッズBEE第9回ファイナルの「もんだい9」に触発されて作りました。麻布や灘2日目のような誘導をきかせたつもりですが,時間はもっとじっくりかけて解いていいと思います。
紙テープの折り重ね方に関する問題。筑駒・麻布的です。
円周を等分する点を直線で結んでいくときの経路の長さについての問題です。
左から見ても右から見ても,「と中までは」回文数になっている整数の問題です。
デジタル数字の応用問題です。
見通しのよい場合分けと,精確な調べ上げが必要です。
数論の発想を使う,図形の回転の問題です。
円周上を動くコマと剰余類に関する問題です。
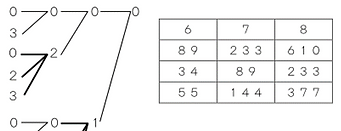
表裏に異なる数字が刻んであるコインを裏返していく
問題です。
表裏に異なる数字が刻んであるコインを裏返していく
問題の第2弾です。
表裏に異なる数字が刻んであるコインを裏返していく問題の第3弾です。
じゃんけんであいこになる場合の求め方を追求する問題です。
じゃんけんをする人の区別を行わない場合に,あいこになる場合が何通りになるかを論及する問題です。
変則的なじゃんけんに関する場合の数の問題です。
あいこの得点を「ストック」しておけるじゃんけんゲームの問題です。近頃の開成にありがちな,「がんばって場合分けよう」というタイプの問題です。
あいこの得点を「ストック」しておけるじゃんけんゲームの問題です。近頃の開成にありがちな,「がんばって場合分けよう」というタイプの問題です。
あいこの得点を「ストック」しておけるじゃんけんゲームの問題です。近頃の開成にありがちな,「がんばって場合分けよう」というタイプの問題です。
渋谷教育学園幕張中2026と同じタイプの,各列に並ぶ数の積が等しくなる問題です。
右下に進むにつれて大きくなる数がならぶ表において2つの和分解を組みあわせた問題です。もともと試行力問題として作成したものの,難度がかなり高いので数字を大きくして最難関仕様にしました。栄光学園のイメージでしょうか。
トーナメントの問題では,試合数は参加人数-1となりますが,それとは別に数量的に扱える事柄を考えてみた問題です。
カードの組合せに関する比較的シンプルな問題です。
となり合わないように座る場合の数を求める問題です。
互いに席を1つ以上あけて座るという気遣いがどういった結果になるかを考える問題です。
一列に並んだ椅子に両隣りに人が座らないように着席する問題です。
横2列に並んだ椅子に,前後左右にとなりあわないように座っていく問題です。
横2列に並んだ椅子において,前後左右のすべてに人が座ることが無いようにする問題です。
椅子の数,人数,選び方の3つの値の間の関係を考える問題です。
隣り合って座ることを避ける問題の円卓版です。
回転対称性について考える,図形の場合の数の問題です。
円順列の問題です。
円順列・数珠順列・異性体が絡んできます。
回転対称性や異性体に注意をして塗り分けの場合の数を求める問題です。
女子学院のマス目に数字を入れるパズルを1次元とすると,その2次元版の問題です。奇数がいくつ入るのかの条件について考えていくので,内容的には麻布・開成的です。
階段状にカードを並びかえる問題の,最難関版です。
奇数・偶数の並び順に関する場合の数の問題です。
角すいの頂点名を入れかえる場合の数の問題です。
数と記号の並び方を変える約束記号の問題です。
○✕の配置の対称性と○✕を置く手順の対称性を考える問題です。配置の「対称性の破れ」が鍵となります。
3目並べの問題の第3弾,もっとも複雑になる,9手目で一列がそろって先手が勝つ問題です。
開成風の,場合分けを積み上げていく問題です。
道を新たに開通することで,道順がどのように変化するかを考える問題です。
道を新たに通す問題です。
道を新たに2本開通する,道順の問題です。
最短距離の道順を模様としてみる問題です。
冊子形式になってからの開成を若干意識した,正三角形のマス目における道順の問題です。
すべての部屋を1回ずつ通過する方法が何通りあるか,長めの文を読みながら説明をする問題です。
さいころを10個振ったときの,2つ,3つずつの目の和について考える問題です。
最終的に同じ記号に収束していく,記号の置き換えに関する問題です。
記号列への操作の途中経過を考える問題です。
三角すい型の魔方陣の問題です。
カードに書かれた数に関する推理の問題です。
月ごとのカレンダーを重ねたときの見え方に関する問題です。
2024のとなりあう位の数の差はすべて2ですが,このような条件を満たす3~5桁の整数の個数を求める問題です。
一筆書きの書き順の問題です。
道順と三角数(などパスカルの三角形に現れる数),三角数の平方数である2025を絡めた問題です。
正方形を重ね合わせた図形における道順の問題です。
円をいくつかの部分に分割する,場合の数の問題です。
2025のカードを裏返しありで並びかえる問題です。
2と5,6と9のカードの回転・裏返しOKで2026を並びかえた4桁の整数について計算をする問題です。
2026の数字カードで作られる整数の順番や総和を考えます。
調べ上げつつ,仕組みを見つける並べ方の問題です。
文章題
a:bの逆比はb:aでよいのに,a:b:cの逆比は順番の入れ替えにならない,という誰しも一度は「ん?」と思う事柄に関する問題です。タイトルが解法のネタバレになってしまうので,問題用紙からはタイトルを抜いています。
比・割合と和差,2つの単元の融合問題であるニュートン算を,思いっきり和差寄りにしてみました。
図のように側面に穴が開いている容器に水を注ぐ,途中からニュートン算になる問題です。設定はシンプルですが,和差系の発想が�重要になってきます。
容器の穴の大きさが底面積に比例する,という仕組みを伴うニュートン算の問題です。
ニュートン算に賃金と利益を盛り込んだ問題�です。
ニュートン算と時計算の融合問題です。
途中から動く歩道の上を進む問題です。
50㎤の水と50㎤のエタノールを混合すると,体積は100㎤より少し小さくなります。減少度合いを簡単に定式化して,重量濃度と体積濃度の関係を考える問題にしました。
水とエタノールを混合すると,体積が少し減ります。
和差系の発想を使う,移動距離の問題です。
条件は単純ですが,論理を積み上げていくことが求められる開成タイプの不定方程式(いもづる算)の問題です。
不定方程式について,論理を積み上げていく問題です。
不定方程式の逆算方法を考える問題です。
以下の式を満たす整数の組を探します。色々な手法を駆使して解説しましたが,何が最善手なのか…作問者にも不明です。
場合分け&不定方程式という,御三家・筑駒などで定番スタイルの問題です。
水と食塩水全体の反比例関係に注目して解く問題です。
水と食塩水全体,食塩と食塩水全体の反比例関係に注目して解く問題です。
水の重さに注目して解く食塩水の問題です。ネタバレになってしまうので,文書データではタイトルが「食塩水の問題」となっています。
食塩水の混合に関する問題です。
食塩水の混合の応用問題です。モーメント計算の考えで解説しています。
定番問題の食塩水の等量交換を,ひねった問題です。
食塩水の応用問題です。抜け道がありそうで怖いですが…。
消費税率と消費税額の変化に関する問題です。
消費税率アップに関する問題の第一弾です。
消費税率が上がったときに税込み価格が変わらない場合,何円か上がる場合,本体価格が上がると税込み価格の差が小さくなる場合などについて扱った問題です。
まとめ買いしてたときとばらばらに買ったときの支払う金額に関する問題です。
消費税率が上がっても,税込み価格が変わらないように本体価格を値下げするキャンペーンの問題です。
消費税と差集め算の問題です。
消費税率アップに関して,一見つるかめ算ふうにまとめ買いを扱った問題です。
消費税・売買損益におけるニュートン算の問題です。
3種類以上の重さの平均をつり合いを考える問題です。
一風変わった平均点の問題です。
比と割合系より手ごわいことが多い,和差系の平均と順位に関する問題です。
平均点と順位に関する和差系の問題です。
平均点以上・未満の人数に関する和差系の問題です。
2位の得点が平均点以下となる場合についての問題です。
こちらは,前後編組の前編で,「とりあえず答えを出す」といった程度です。
2位の得点が平均点以下となる場合についての問題です。
こちらは,前後編組の後編で,仕組みについて考えます。
ベン図が使えなくなる,4種以上の集まりの問題について深めてみました。
2人が同じ舟や別々の舟に乗って,すべての舟を対岸に運ぶ問題です。
開成中で1993年に年令算と誕生日の問題が出題されました。「既存の問題を精緻化する」という開成らしい作問作法に基づきつつも,当時の開成は出題数が多かったので難易度は低めでした。今回は少しだけ手ごたえのある問題にしています。
誕生日がわかっていて,現在の日にちはわからない条件下で考える年令算の問題です。
おまけの問題を逆算タイプにしてみました。
差集め算と調べ上げを複雑に組み合わせた問題です。
人数が異なっても1人あたりに分配される個数は変わらない場合について,いろいろと考える問題です。
和分解&順位系のよくある問題の発展問題です。
色々な累乗数を素数11で割ったときの剰余に関する問題です。
各位の数を,となりあう位の数の差に置き換えていく問題です。階段状に積み上がる構造を追っていきます。
数の性質
連続する整数の積とパスカルの三角形の問題です。
a×bをある数で割ると三角数(2次元)
a×b×cをある数で割ると三角すい数(3次元)
a×b×c×dをある数で割ると五胞体数(4次元)
長大です。
単位分数に分解する式の個数を,分母の素因数分解から求める方法を,考察・証明する問題です。
範囲から総当たりで探すよくある手法とは全く異なります。
単位分数に分解する式の個数を,分母の素因数分解から求める方法を,考察・証明する問題の第2弾です。
範囲から総当たりで探すよくある手法とは全く異なります。
単位分数に分解する式の個数を,分母の素因数分解から求める方法を,考察・証明する問題の,2023版です。
範囲から総当たりで探すよくある手法とは全く異なります
単位分数に分解する式の個数を,分母の素因数分解から求める方法を,考察・証明する問題の,2024版です。
範囲から総当たりで探すよくある手法とは全く異なります
N進法の小数を用いて,すべての分数(有理数)を有限小数で表す方法を考える問題です。単元研究「N進法の整数と小数」の最終部分をまとめたものです。
受験算数界隈でたまに見かける「鳩の巣原理」「ディリクレの部屋割り論法」を利用した数の性質の問題です。
継子立てについて,成立する条件と理由を説明する問題です。
下のような,桁を入れかえる一般的な計算式を考察する問題です。
3桁の整数abcが(a-b+c)の倍数となる場合についての問題です。
開成中・平成17年のN進法の問題の設定を変えて,N進法とは異なる位取り記数法を模索する問題にしました。
開成中・平成17年の問題の設定を変えて,N進法とは異なる位取りを展開する問題の第2弾です。
10進法と8進法が混ざり合った問題です。
下の図のような天秤でもれなく整数グラムを量るために必要な分銅に関する問題です。
おもりのつり合いとN進法の問題を一般性の下に扱おう,という問題です。
いくつかの数字の並びを指定したN進法の整数について,残りの位の埋まり方を考える問題です。
N進数と多角数の関係について考える問題です。
異なるN進法で同一の数表現がどのような値を意味するのか,についての問題です。
フェルマーの小定理を証明する問題です。
リフルシャッフルを合同算術で考える問題です。
長方形と正方形を利用して,算数で2次方程式を解く問題です。
2021の開成中入試問題のように,分数と小数,特に循環小数でよく出題される無限級数の問題を,買い物のポイントという設定にしています。
整数を,連続するn個の整数に和分解できる場合の,n以外の個数に関する問題です。
連続する奇数の和に関する問題です。
整数を連続する整数の和に分解する問題はよくありますが,こちらは奇数か偶数の和に分解する問題です。
15=5+6+7のような連続する整数への分解について,最も多くの整数に分割される場合に特化して仕組みを考える問題です。
連続する整数への和分解の応用問題です。
2つの素数の積である半素数を,連続する整数の和に分解する問題です。
2026と同じく,連続する整数への和分解が1通りかつ偶数個となる整数について考える問題です。
整数の各位の数の和と積の大小関係に関する問題は,関東・関西ともに最難関校では外せない問題です。深いところに切り込む必要性を感じて作った問題です。甲陽学院の改題を導入問題として添えています。
和と積の大小関係に関わる問題です。
式の答えの各位の数の和を求める問題です。秀逸な2020年甲陽学院2日目大問1(1)に着想を得ました。
11…11を2個掛け合わせてできる積に関する問題です。
5列に自然数をならべた数表において素数の配置を考える問題です。
6で割ったときの余りが1になる素数(つまり6を法として7と合同な素数)についての問題です。
約数の個数が4個である整数を数え上げるために,素数判定を行います。
73の倍数の見分け方を与えたうえで,分母73の分数について考える問題です。
19の倍数で以下の形となる最小の整数を求める問題です。
17の倍数と7の倍数の見分け方とその組み合わせについて考える問題です。
根基10の整数(素因数が2と5のみである整数)と根基6の整数がどのように散らばっているかを考える問題です。「埋め込み」の構造を見て取ることができます。
根基21の整数(素因数が3と7のみである整数)の配置と,剰余の関係を考える問題です。
根基が6の整数と15の整数の和の性質に関する問題です。
根基が6の整数(素因数分解して2と3のみが現れる数)より2大きい数についていろいろと考えていく問題です。
2023=7×17×17ですが,7分の1も17分の1も循環小数として大変きれいな性質を持っています。この問題では,17分の1を利用します。
2024=8×11×23です。11も23も
9999999999999999999999の約数であることを利用する問題です。
2025=81×25であることを利用した,循環小数の問題です。
分母2025の分数と循環小数をあしらったグッズを販売しております。
分母2025の分数と循環小数の問題の第2弾です。
下のような分数列の和に関する問題です。
分母が連続する整数の,3つの単位分数の和に関する問題です。
2024で割ると917余る三角数を求める方法について考えていく問題です。
累乗によってできる数をほかの数で割った場合の余りについて考える問題です。
色々な累乗数を素数11で割ったときの剰余に関する問題です。
もとの数と累乗の回数を色々と変える(つまりaのn乗)を
7や11で割った余りについて考える問題です。
連続する整数の積が2で割れる回数についての問題です。
奇数列の和の特徴を利用して素因数分解をしよう,という問題です。
剰余の性質に注目をして,不定方程式の答えを探す問題です。
等比数列をあるきまった数で割ったときの剰余について,くり返しが起こる「まで」について考える問題です。
等比数列をある数で割った余りの数列についての問題です。
等比数列について,剰余にかかわる性質を色々と考える問題です。
直角三角形の3辺の整数比を無数に算出する方法を考える問題です。
最大公約数12・最小公倍数360になる整数の組合せについていろいろと考えていく問題です。
3個の整数の公約数・公倍数に関する応用問題です。
3個の整数の公約数・公倍数に関する応用問題です。
2012年に開成中で「2番目に大きい約数」に関する問題が出題されました。いろいろと条件を変えると大いに広がりができる主題ですので,変奏してみました。
2番目はともかく3番目にするとかなり複雑になります。じっくり解きたい子向けです。
灘中2002年2日目の問題を少しずついじっていこう,という問題の第2弾です。
約数と,約数の逆数に関する問題です。
素因数分解と素数の個数に関してあれこれと考える問題です。
素数の個数と素因数分解についていろいろと考える問題です。「素数の個数と素因数分解・1」を先に解いておくことをお薦めします。
整数の列を単位分数の列に変換する問題です。
単位分数の通分について,簡潔な説明を行う問題です。
単位分数への分解を,逆数に絡めた問題です。
分母が2026や3039の分数を単位分数の和の形で表す問題です。
a+b=cのときのa,b,cの逆比について成り立つ意外な性質について考えていく問題です。
一の位が等しいいくつかの整数の積の下2桁に関する問題です。
2023を含めて,積の下2桁が23になる整数の組みあわせについて考える問題です。
剰余類を組みあわせて考える問題です。
カードを置き換えていく問題です。倍数や素因数をそこそこハードに考えることが求められます。
カードの置き換え操作に関する低学年用の問題を高学年向けに作り替えたところ,過去に公開した問題と設定が完全にかぶってしまった問題…もったいないので公開します。
不定方程式の逆算方法を考える問題です。
小正方形を対角線が通過する問題で。何番目に度の小正方形を通過するかを問います。
小立方体を対角線が通過する問題で。何番目にどの小立方体を通過するかを問います。
小立方体を対角線が通過する問題で。何番目にどの小立方体を通過するかを問います。
対角線が通過する正方形や立方体の個数の問題は,本質的には分数列の問題でしょう,という考えに基づいて作った応用問題です。分数列の考えを理解するための導入問題をつけました。
デジタル数字の2020を並べたマス目に引いた対角線が通過する正方形と長方形の個数に関する問題です。
対角線とは少しずれた直線が通過する小正方形の個数の問題です。
球の反射の問題と,長方形の対角線が通過する小正方形の個数に関するいわゆる「レーザー光線」の問題の融合問題です。
2点しか通過しない直線の本数に関する問題です。
正方形の辺および内部にある点の個数に関する問題です。ピックの定理ではありません。
真分数である既約分数の個数に関する問題です。
例えばある分母の真分数である既約分数が14個ということはあり得ない,という問題です。
等分割したいろいろな円=分数列を自由に重ね合わせる問題です。
等分割の問題を,往復の状況下で考えます。
素因数をたし算する問題です。
約数の和の公式への誘導を経て,逆算系の発想に持ち込む問題です。
部分分数分解の応用問題です。
1/2020=1/4×101×5=1/404-1/505を利用した,部分分数分解の問題です。
2020=2×2×5×101であることから,分母を4数の積でとらえる部分分数分解とからめてみました。
2024と部分分数分解の問題です。
分母が2025の分数を部分分数分解する問題です。
2026=2×1013なので,部分分数分解の解として扱いやすいです。
分子が1の分数を単位分数といいますが,分子が2,3についても条件に加えてみた問題です。
2020と単位分数の問題です。
分数を和分解する問題です。
2023以降の年号から帯分数,仮分数を作る問題です。
同じ曜日なら7で割った余りが同じ,ということを利用する問題です。
カレンダーの各週から日にちを1つずつ選んで和と差を考える問題です。剰余類の発想を利用します。
カレンダーの各週から日にちを1つずつ選んで和と差を考える問題の第2弾です。剰余類の発想を利用します。
カレンダーの日付けに関して,剰余類の発想に基づいて和分解を行う問題です。
1年間のカレンダーをつなげた状態で,剰余類について考える問題です。
12か月分をつなげたカレンダーにおいて,図のような枠で日付を囲む問題です。
12か月分をつなげたカレンダーに関する問題の第3弾です。
マヤ文明の歯車式カレンダーに着想を得た問題です。
よくある,切手の組み合わせによる剰余類の問題を,逆算問題にしてみました。
切手の組み合わせによって作ることができない金額について,剰余類に注目した表で解くことは一般的です。この問題では,その表におけるズレの動きに注目をします。
切手の組み合わせによって作ることができない金額を考える剰余類の問題の,発展問題です。
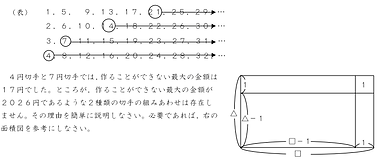
2種類の切手の組みあわせでつけれない最大の金額が2026円,というパターンは存在しないことを説明する問題です。
以下の式を満たす整数の組を探します。色々な手法を駆使して解説しましたが,何が最善手なのか…作問者にも不明です。
剰余に注目して不定方程式を解く問題です。
小数の割り算における,商の桁数と余りに関する問題です。
2023を整数で割った商に関する問題です。
時針・分針・秒針が正多角形の頂点になる条件に関する問題です。必要とされる考え方を鑑みて,速さではなく数の性質に入れました。
かけ算の筆算を利用する虫食い算の問題です。
虫食い算と場合の数の問題です。
素因数分解・数の範囲等を考えて場合分けを行う問題です。
1けたの整数どうしの積の大きさに関する問題です。
各位の数の間に+-×÷を入れて計算結果が最大となるようにする問題です。並び方によって最大値が異なる点に注意をします。
余り,余りの余り,余りの余りの余りについて分け入る数・規則の問題です。
分母7の分数を参考にして,分母21875の分数を小数で表す問題です。
分母が31の分数を循環小数に展開する問題です。
2020=2×2×5×101,2×2×5=20については1÷20=0.05,101は回文数であり1÷101=0.00990099…と,なかなかに整った数であると言えそうです。
2020に関する問題をいくつか作っていきます。
前回(2020の問題・1)の続きです。
2020は❛20❜を繰り返しています。このような「繰り返し数」に関する問題です。
2020を色々なN進法・位取りで表してみる問題です。
2020の色々な倍数について,約数の個数を考える問題です。
2024を整数倍した数の約数の個数に関する問題です。
2020の約数である101の倍数の,回文数を考える問題です。
以前に試行力問題で出題した,2020を並べた数列の1か所に+を入れた答えについて考える問題のハイレベル版です。
20252025を’+’で区切った計算結果について考える問題です。
2020の各位の数を入れかえてできる数の和に関する問題です。
よくある各位に並ぶ数を入れかえる問題をいろいろとアレンジします。
数字のならび方に条件を入れた,けた入れ替えの問題です。
2けたごとの並びかえを行っても8の倍数のままであるような整数に関する問題です。
2026の各位の数を入れかえてできる整数の和をめぐる問題です。
整数の各位の数を入れかえてできる整数の和が回文数になる条件について考える問題です。
各位の数を入れかえる問題と,N進法の融合問題です。
10進法以外の場合で各位に並ぶ数について考える問題です。
N進法と,各位の数の並びかえの問題です。
5進法で特定の位の数を指定する問題です。
343010に現れる2つの3は,それより下の位にある3より小さい数が3個になっています。ふつうの整数をこのような性質をもつ数に変換する手順に関する問題です。
数がその個数分だけ現れる整数に関する問題です。
有限小数の一番下の位について考える問題です。
各位の数の和が等しい小数の大小関係に関する問題です。開成中のあまり難しくない問題をイメージしています。
分子が2,分母が5の累乗数である分数を小数にしたときに並ぶ数に関する問題です。
奇数番目の多角数は,必ずその奇数の倍数となることを説明し,その性質を利用して問題を解いていきます。
偶数角数の偶数番目について,倍数の性質を考える問題です。
三角数でも四角数でもある数(1,36,…)を求める問題です。
三角数=四角数をあしらったグッズを販売しております。
六角数を三角数と関係づけて,隣どうしの和を求める問題です。
三角数と平方数と立方数の関係を考える問題です。
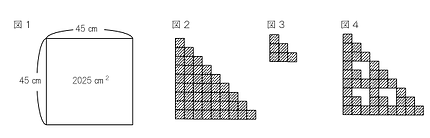
定番すぎるものの外せない,2025が45×45という三角数の平方数であることと立方数の関係の問題です。
2025が三角数45の平方数であることから,三角数の平方数の性質について考えてみました。
126で割ると96余る三角数について考える問題です。
黄金比によって生成されていく黄金長方形について,多角数の問題にしてみました。
図のように三角すい状にならべた点の数を多角数の文脈で考える問題です。
三角すいを構成する頂点の個数という多角数的な数と,かけ算九九の関係を考える問題です。
三角数と奇数平方数の関係を利用する問題です。
三角数と五角数に相当する階差数列の関係を利用しながら,どんな整数の倍数になるのかを考える問題です。
三角数について,3で割れる回数を考える問題です。理由を説明する設問もつけています。
素数の三角数について説明をする,コンパクトな問題です。
整数をトーナメント状に三分割する問題です。桜蔭中2019年入試の3人トーナメントの問題に着想を得ています。
素因数分解と整数の範囲に関する問題です。
回文数が分布する頻度を,隣りあう回文数の差から考える問題です。
回文数が分布する頻度を,隣りあう回文数の差から考える問題です。
整数部分-分子-分母をつなげると回文数になるような分数に関する栄光学園のような,パズル的問題です。
整数部分-分子-分母をつなげると回文数になる分数に関する問題です。
大きな水槽に小さな容器を複数回使って水を入れる問題です。実質的に数の性質の問題です。
連続する整数の和に関する問題です。
平方数の差と,連続する整数の和に関する問題です。
積み木の組み合わせ方から,立方数の差について考える問題です。
2025は平方数,2027は素数です。
2個の素数の積である整数を,半素数といいます。2026も半素数です。半素数と約数の和に関する問題です。
平面図形
方眼を利用して,3辺が整数比となる直角三角形を作る問題です。
3辺が整数比の直角三角形シリーズをあしらったグッズを販売しております。
3辺の長さの比が整数比となる直角三角形の問題の第2弾です。
3辺の長さの比が整数比となる直角三角形の問題の第3弾です。ここで得られる方法に基づいてピタゴラス数を算出するエクセルシートは,「ツール」のページで公開しています。
3辺の長さの比が整数比となる直角三角形の問題の第4弾です。今回はピタゴラス三角形から新たなピタゴラス三角形を作り出します。
折り返しから,ピタゴラス比に行き着く問題です。
シンプルな設定から,以下の3つを示します。
① (2×a×b):(b×b-a×a):(b×b+a×a)
はピタゴラス比
② 角Bが直角である直角三角形ABCについて,
AB:(BC+CA)=a:bが整数の比のとき,
AB:BC:CA=
(2×a×b):(b×b-a×a):(b×b+a×a)
③ ピタゴラス三角形の3辺の比は,
(2×a×b):(b×b-a×a):(b×b+a×a)
の形で表すことができる
3辺が整数比の直角三角形・6をあしらったグッズを販売しています。
図の直角三角形のb,c,にあてはまる整数の組をすべて求める問題です。
図の直角三角形ABCの残りの2辺の長さとしてあてはまる整数の組をすべて求める問題です。
ピタゴラス三角形と,内接円の半径の長さの間に成り立つ関係を考える問題です。
ピタゴラス三角形と,それに内接する円についての問題です。
途中でピタゴラス数が現れる図形の問題です。
60度ないし120度の角を持ち,3辺の長さが整数比となる「アイゼンシュタインの三角形」を無限に生成する方法を考えます。
1つの内角の大きさが60度か120度で,3辺の長さの比が整数比になる,「アイゼンシュタインの三角形」を無限に生成する方法を考えます。
長方形・正方形と黄金分割の問題です。
黄金分割に基づく図形から,フィボナッチ螺旋を構成する問題です。
黄金分割に基づく図形から,フィボナッチ螺旋を構成する問題です。
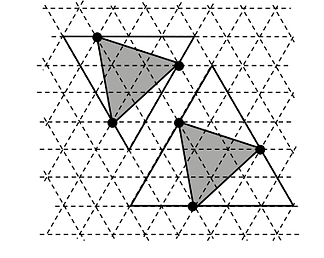
正三角形を用いたパズルは算オリ・最難関中入試において,常に警戒すべき問題です。
正三角形シリーズの第2弾です。
正三角形シリーズの第3弾です。傾けた3つの時計の問題です。
図のように三角形を回転させる問題です�。
正三角形に関する問題の第12弾です。
1辺が1㎝の円を組みあわせた以下の図形において,斜線部分の六角形の面積を求めることができる,という問題です。
正六角柱を切断する問題です。通常の3つの手順では解けないようにしてあります。
下の図の3つの円の半径を求める問題です。
正三角形シリーズの16本目,六角形を回転させます。
円が内接する正三角形において,面積の関係を細かく考えていく問題です。
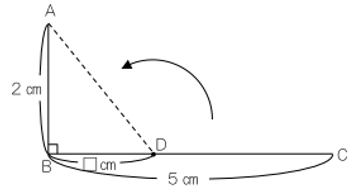
下の図において長さの比□:△を求める問題です。
正六角形を少し回転させたときにできる三角形について考える問題です。
正三角形と等脚台形の重なりに関する問題です。
正三角形の一部分の等脚台形の面積を求める問題です。
正三角形と半円を組みあわせた問題です。
ひし形に内接する正三角形の問題です。
下の図において3点B,C,Dを通過する円の面積を求める問題です。
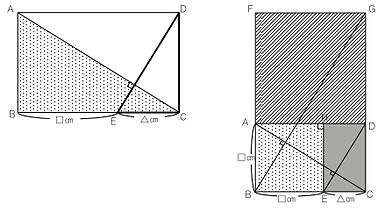
正三角形を敷き詰めた平面において長方形を直定規1本で作図する問題です。
正三角形と正六角形の長さについてのパズル問題です。
図1→2→3と平行に棒を離していくときの面積の関係を考える問題です。
図の2つの正三角形がAP:PD=CP:PB=3:1となるときの面積比を求める問題です。
正三角形のマス目上で正三角形を作図する問題です。
正三角形に内接する二等辺三角形の面積の問題です。
下の図においてAE=BEのとき,2つの正三角形の面積比を求める問題です。
重ねた2つの正三角形の面積比を求める問題です。
正三角形を拡張して作ることができる三角形の面積に関する問題です。
正三角形シリーズ35
下の図の2組の線分比から,2つの正三角形の面積比を求めます。
図の小さな円の面積を求める問題です。
図①の長さを与えた場合に,図2の二等辺三角形と正三角形の面積の比を求める問題です。
アイゼンシュタインの三角形の発想も用いて解く折り返しの問題です。
正三角形シリーズに,アイゼンシュタインの三角形の発想を取り入れた問題です。
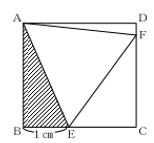
図の三角形の面積から,AC+BCの長さを求める問題です。
入れ子状の正三角形の面積比・線分比の関係を考えます。
下の図の2つの三角形の面積比から,線分比を求める問題です。
1つの内角が60度の三角形の辺の長さに関する問題です。
下の図のかげをつけた正三角形は,辺の傾き方から,(1,3),(2,3)の2通りに表すことができます。このような表し方について考えます。
下の図において,AB:BD:DC=15:5:7のときの角アの大きさを求める問題です。
下の図の,アの角の大きさを求めます。
三角形ABCが正三角形のときに,アの角の大きさを求めます。
作るのは楽,解くのは大変かもしれない角度の問題です。
定規とコンパスでは作図不能な,角の三等分に関する問題です。
作図が不可能であることがしられている,角の三等分に関する問題です。
麻布・筑駒のイメージの問題です。最難関問題は模試では使えないレベルの問題が多いのですが,本問題は模試でも使える設定です。
6つの辺の長さが等しい「六等辺六角形」の探し方についてマス目の上で考える問題です。
下の図の三角形の面積を求める問題です。
円周角タイプの問題設定において,面積について考える問題です。
円周角タイプの問題設定において,面積について考える問題です。
正三角形の高さが1辺の長さの7/8倍より低いことを説明せよ,というシンプルな問題です。
正六角形を重ねてできる花の形が相似であり続ける,ということを利用して解く問題です。
斜線の四角形の面積から,円の面積を求める問題です。
下の図の三角形の3辺の長さとHPの長さから,内接円の半径を求める問題です。
三角形の五心のひとつ,垂心についての問題です。
正五角形の内部の分割において現れる特別な比の問題です。正五角形は正六角形より影が薄いですが,実はすごい図形です。
図の長さの設定下で,対角線ADの長さを求める問題です。
正七角形の1辺の長さと対角線の長さから,図の影の部分と正七角形全体の面積の比を求める問題です。
正九角形の対角線の長さについての問題です。
正九角形と,内部の正多角形の面積比を考える問題です。
近似値を利用して,正九角形内部の二等辺三角形の面積の比を求める問題です。
図の斜線部分の面積を求める問題です。
気づけば一瞬,4年生でもあっさり解けます。
正八角形の分割問題の第2弾です。
正八角形の分割に関する問題の第3弾です。麻布・開成の入試問題と同様のスタイルになっています。
下の図の斜線部分の面積を求める問題です。
正八角形の分割に関する問題の第5弾です。麻布・開成の入試問題と同様のスタイルになっています。
かげをつけた部分の面積の和を求めます。
斜線部分の五角形の面積について考えます。
正八角形に内接する円の面積を求める問題です。
直角三角形の3辺の整数比を無数に算出する方法を考える問題です。
正方形と正八角形を敷きつめたマス目上で正方形の面積を考える問題です。
正方形と正八角形を敷きつめたマス目上で正方形の面積を考える問題です。
「円による図形の反転」についての問題です。
面積が決まっている直角三角形の頂点を,定規とコンパスで作図する問題です。渋谷教育学園幕張などの受験生にはおすすめです。
図の太線SQが通過する部分の面積を求める問題です。
作図の問題です。
図の斜線部分の面積を求める問題です。
円を実質的にマス目の上において考える問題です。算数オリンピック系の発想で,2020年の麻布の問題もその変種といえます。
60度に傾いた複数の直線でおうぎ形を分割する問題です。
見るからに麻布的な設定で,正三角形に関連する図形を色々と見出す必要があります。
3つ円の重なりと,「幾何平均」の考えを利用する問題です。
□にあてはまる整数を求める問題です。
下の図の□の長さを求める問題です。
下の図において,円の半径を与えたうえでx,yの長さを求める問題です。
下の図においてBF:FE=36:41であることから,AFの長さを求めます。
BE=BFである二等辺三角形が長方形に内接する問題です。
図の台形ABEFの面積を求める問題です。
長方形・正方形・おうぎ形の複合図形において面積の関係を考える問題です。
円の中心が長方形の対角線上にくるように2つの図形を組みあわせたときの面積と長さの比について考える問題です。
下の図の正方形の面積を求める問題です。
正多角形と角度に関する問題です。図の角アの大きさを求めます。
おうぎ形を斜めに動かしたときに,弧が通過する部分の面積を求めます。
おうぎ形を斜め方向に平行移動させる問題です。
輪が正方形の周りを回る際に通過する部分の面積を求める問題です。正三角形や直角二等辺三角形の問題はありましたが,正方形でも解けるんです。
円が回転したときの接地距離について体系的に考えます。一度まとめておきたかったので。
回転効率をあしらったグッズを販売しております。
天動説に強い説得力を持たせた幾何学的装置である周転円に関する問題です。円周上を別の円が回転移動します。
天動説の周転円のように,円が回転しながら円周上を進む問題です。
二重の円板を回転させる問題です。
すべり台の下から上に向けて箱を滑らせる問題です。
円が円の周りを回転する問題です。
正三角形が向きを変えることなく円周に接しながら一周する問題です。
正三角形が円の内部を向きを変えることなく移動する問題です。
正方形が図のように平行移動したときに,1つの頂点が通過したあとの長さを求める問題です。
正方形が向きを変えずに円の周囲を回る問題です。
中心角が60度のおうぎ形を3つ合わせてできる「ルーローの三角形」に関する問題です。
おうぎ形を組み立てて作った「五角形」の回転に関する問題です。
ルーローの三角形を,敢えて平行移動させてみる問題です。
灘中2002年2日目の問題を少しずついじっていこう,という問題の第1弾です。
灘中2002年2日目の問題を少しずついじっていこう,という問題の第2弾です。
灘中2002年2日目の問題を少しずついじっていこう,という問題の第3弾です。
円や正方形の代わりに,おうぎ形を直角三角形の内部で移動させる問題です。
円や正方形の代わりに,おうぎ形を直角三角形の内部で移動させる問題です。
円が円のまわりを転がるときの回転数の問題はよく出題されますが,こちらは正方形が円のまわりを転がるときの回転数の問題です。
円の内部を正方形が向きを変えずに移動する問題です。
図形が円周上を向きを変えることなく移動する問題です。
円周上の平行移動をあしらったグッズを販売しております。
らせんを描くように図形が回転する問題です。
方眼のらせんを描いて正三角形が回転する問題です。
正方形を螺旋にそって回転させたときにできるいろいろな模様に関する問題です。
らせんと回転・正方形をあしらった
グッズを販売しております。
今年(2025年)の筑駒で,正十二角形の内部を正三角形が回転する問題が出題されたので,類似の問題を作成しました。
正十五角形の内部を図のように正三角形が回転します。
細い棒を周期的に回転させることで出来上がる図形について考える問題です。
色々な角度で回転していく棒が描く形と面積について考える問題です。
色々な角度で回転していく棒が描く形と面積について考える問題です。
正十五角形の外周を正方形が回転する問題です。
正六角形と長方形が向かいあって回転する問題です。
正方形が平行・回転移動していく問題です。おうぎ形の面積の比と中心角の関係,等を細かくまとめていきます。
図形上の円の移動に関連する,周期とやや面倒な求積の問題です。
正六角形の辺上を正三角形が平行移動し,正三角形上を点が移動する問題です。
円周上の点と多角形の頂点の重なりについての問題です。
パックマンのような形のおうぎ形が図形の内部を自由に平行移動する問題です。桜蔭,栄光などをイメージしています。
直角三角形の回転を細かく見ていく問題です。
正三角形を組み合わせた図形を回転させる問題です。
正三角形を組み合わせた多角形の回転移動の問題です。
正三角形を並べたマス目における回転運動の問題です。
昭和58年の麻布中のさやがた文様の問題を,2020のらせん模様で改題してみました。
図形の対称性と場合分けの問題です。
相似の1種である影の問題の応用問題です。
坂道(階段)において影の先端の速度変化を考える問題です。
バウンドする2つのボールの影に関する問題です。
折り返しにおける,直線の傾き関係についての問題です。
正六角形と線分比・面積比の応用問題です。
一度ははっきりと確認しておきたい,台形の相似に関する問題です。
正多角形の面積の関係に関する,シンプルな問題です。
正三角形のマス目上でいろいろな長方形を作る問題です。
長方形の回転移動において角頂点の移動距離の関係を考える問題です。
正六角形を何回転もさせるときの,各頂点の移動距離に関する問題です。
下の図形を「少しだけ」回転させる問題です。
おうぎ形を組み合わせたきのこ型図形の回転移動の問題です。
合同なおうぎ形を組み合わせた図形を回転移動させる問題です。
紙の折り重なった枚数について細かい分析を行う問題です。
電灯光の影の問題において,逆比を活用する問題です。
おうぎ形の内部を円が自由に移動する問題です。
正六角形内部に置いた仕切りによって見えなくなる部分の面積を求める問題です。
円がジグザグの経路を移動する問題です。
麻布の円の問題を難しめに改題してみました。
麻布中平成23年の輪と正三角形に関する問題を変奏してみた問題の第2弾です。
平成23年に麻布中が輪が正三角形のまわりを動く問題を出題しました。こちらは輪が正二十角形のまわりを自由に動く問題です。
2020の形をした図形を平行移動させる問題です。
方眼上での3点の間の道のりに関する平面図形の問題です。
三角形の内側に直角二等辺三角形が入っている問題です。
角度の問題でよくある下の図形において,線分比を考える問題です。
下の図の三角形ABCの面積を求める問題です。
図の斜線部分の面積を求めるシンプルな問題ですが,いろいろと考えなければなりません。
下の図の直角二等辺三角形ABCの面積を求めます。
図のAE:ECを求める問題です。対話式の誘導を入れています。
相似,辺の傾きと垂直の関係を利用する問題です。
直線の垂直と傾きの関係を利用する相似の問題です。
正方形と,直線の垂直関係を利用する問題です。
AC=DCである下の図において,三角形ABCの面積を求める問題です。
折り返しの,比較的平凡な応用問題です。
等積変形と,相似の考え方を組みあわせた問題です。
下の図において二等辺三角形ABCの面積を求める問題です。
下の図の円の半径および斜線部分の面積を求める問題です。
回転において通過したあとの面積から,回転の中心の位置を考える問題です。
直線の傾きかたを利用する問題です。
直角三角形を2つ組み合わせた平面図形と比の問題です。
図におけるアの長さを求める問題です。開成中2017年のように,比に関する抽象度の高い問題です。
名前の通り,二辺挟角の相似を利用する問題です。
四角形は内角が等しくても相似にはなりません。ですが,いくつかの情報を組み合わせることで確定できる値もあります。
図の四角形においてECの長さを求める問題です。
下の図の五角形の面積を求める問題です。
下の図の四角形ABCDの面積を求める問題です。
正方形��の回転と,間に挟まれる円の関係を考える問題です。
「調和平均」と図形に関する問題です。事前の知識は必要ありません。
幾何平均という考えを用いて,下の図の正方形ADEFの対角線の長さを求める問題です。
下の図において,アとイの長さの比と,色のついた正方形の面積の比の関係を見抜く問題です。すっきりしているというか,かなりシンプルです。
図のア,イの面積の差を求める問題です。
正方形を区切ってできる長方形の面積に関する問題です。
長方形全体と斜線部分の三角形の面積比から,長さの比
AE:EBを求めます。
下の図において,正方形EFGHの面積を求める問題です。
下の図の四角形の面積を求める問題です。
接して並ぶ複数の円の中心を結ぶ線の傾きを考える問題です。
正三角形の内部に作った六芒星の面積に関する問題です。
線対称と回転対称性の関係を考える問題です。
線対称と回転対称性の関係を考える問題の第2弾です。
面積の比と高さの比の関係に集中した問題です。
高さの比に注目して解く問題です。
ひし形内部で合同を利用する問題です。
少し見えづらい直線の平行関係に着目する問題です。
下の図においてAE:EB=1:3のときの,BCの長さを求める問題です。
入れ子になった長方形と面積のパズル問題です。
入れ子になった長方形の内部に正方形ができる問題です。
下の図のよくある正方形と正方形の組みあわせについて,面積の関係を考える問題です。
入れ子になった正方形の面積と整数の問題です。
組みあわせた半円上を動く2点間の距離の問題です。
玉の反射の問題を,長方形や正三角形ではなくて直角三角形で作成しました。対称性がない図形なので,問題が成立する条件が厳しめです。
反射と直角三角形・1をあしらったグッズを販売しております。
直角三角形内部における反射の問題です。
切れ目の入った方眼を切断する問題です。
小さい球が多角形の中を反射する問題ですが,多角形が対称性を持たないために,いろいろな鏡映しの形を考えなければなりません。
平行四辺形の内部を球がいろいろと反射する問題です。
反射を図形のパズルの感覚で解く問題です。
小円が反射を繰り返しながら重なりあう問題です。小円の軌跡と速さの両方を考えることが必要になります。
正方形の辺上のいくつかの点からの近さの範囲について考える問題です。
正多角形の各頂点からの近さの範囲に関する問題です。正90角形まで考えます。
直角三角形の内部を自由に動く円と,各頂点との距離に関する問題です。
二等辺三角形内部にできる三角形の面積と頂点の位置に関する問題です。
円と長方形が接する図形において,3:4:5以外の整数比の直角三角形を作り出す問題です。
円と接する長方形において,細かく比を求めていく問題です。
少し変わった切り口でピタゴラスの定理を実質的に証明してしまおう,という問題です。予備知識として定理を知っていても,問題を解くうえでは特に役立たないようになっています。
マス目上の正方形の面積から,ピタゴラスの定理を証明する問題です。
正方形と,1つの内角が15度の直角三角形を組みあわせた図形の応用問題です。
長方形を対角線の方向に平行移動させる問題です。
立体図形
全ての面が正多角形の多面体,アルキメデスの立体の問題です。
アルキメデスの立体をあしらったグッズを販売しております。
投影・射影が鍵となる,立体の求積問題です。
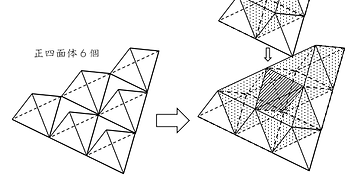
立体&場合の数の問題です。正四面体・正八面体の積み木をできるだけ少ない箇所で糊付けします。
四面体の高さを,正三角形のマス目を利用して求める問題です。
正三角形を並べたマス目上で四面体の展開図についていろいろと考える問題です。
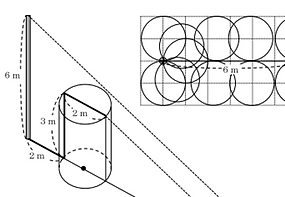
2009年の栄光学園や2020年の甲陽学院2日目で出題された,円柱のまわりに糸を巻く問題の仕組みを考えてみました。
切断面から立体を復元する問題です。
切断面と立体の関係を考える,開成的な問題です。
正四面体の切断面の面積から,体積を求める問題です。
立方体の切断面の面積を求める問題です。
立体切断における切断面の面積に関する問題です。
正六角柱を切断する問題です。通常の3つの手順では解けないようにしてあります。
正六角柱を切断する問題の第2弾です。通常の3つの手順では解けないようにしてあります。
三角すいについていろいろな面・切断面から考えていく問題です。
立体図形の一部分を展開図のように平面図形に落とし込みながら,相似を利用する問題です。
正八面体の容器に水を入れる問題です。
1つの面を床につけた正八面体を真上から見たり切断したりする問題です。
正八面体を回転させつつ,投影を利用して考える問題です。
仕切りのある容器を,一点のみ床につけて傾ける問題です。
斜めの仕切りのある容器を,一点のみ床につけて傾ける問題です。
複雑な仕切りのある容器を,一点のみ床につけて傾ける問題です。
傾けた容器に水を注いだときの水面が,真上からどのように見えていくのかを考える問題です。
傾けた容器を真上から見たときの水面についての問題です。
小立方体の切断面の形について,今一つこなれない解説が多い気がするので,作りました。
小立方体を組みあわせた直方体を切断したときの,切断面の形に関する問題の第2弾です。基礎となる考え方は「小立方体の切断面・1」で説明をしているので,そちらを先に解くことをお薦めします。
電柱の位置を変えることで,板の影の形がどうなるのかの地図をつくります。
展開図からどのような長さを持つ立体ができるのかを細かく考えていく問題です。
柱体と錐体の影について考える問題の第1弾で,角柱の影と角すいの影の違いについて扱います。
電灯光による角すいの影に関する問題の第2弾です。円すいの影同様に,柱体の影とは異なるとらえ方が必要になります。
円柱と円すい,影のできかたはけっこう異なります。
円すいの影に関する問題です。以前に公開した円柱・円すいの影の問題を先に解くことをお勧めします。
円柱と円すいの影のでき方の相違に関する問題です。
円柱・円すいの影・2をあしらったグッズを販売しております。
壁にできる円すいの影の面積に関する問題です。以前に公開した「円柱・円すいの影」を踏まえているので,そちらを先に解くことをお薦めします。
円周角タイプの問題設定において,面積について考える問題です。
2枚の円板の影の重ねあわせ等に関する問題です。
影の長さと範囲に関する問題です。
四角すいの高さと,四角すいに映る影の様子について考える問題です。
厚みのある窓を通って差す光の問題です。
厚みのある窓を通過する光に関する問題です。
厚みのある窓を通過する光に関する問題の第3弾です。
展開図からどのような立体ができるかを考える問題です。
円すいの代わりに角すいを転がす問題です。
角すいを寝かせて転がす問題です。
円すいの展開図と正方形に関する問題。他の問題と比べてライトです。
正方形を色々な仕方で切って三角すいを作る問題です。
容器の傾けと水面の高さに関する問題です。
立方体の容器を斜めに傾けたときの水面に関する問題です。
立方体の容器を斜めに傾けたときの水面に関する問題です。
頂点の重なりの条件にしたがって展開図を完成させる問題です。
立方体を組み合わせたときにねんど玉が何個見えるか,という問題です。
直方体の体積を二等分する方法について考える問題です。
水面変化と水量変化の融合問題です。
直方体を組み合わせた立体を次々と水そうに沈めていく問題です。
徐々に高くなっていく棒を水そうに沈めていく問題です。
底に穴の開いた容器を動かしたときの水の動きに関する問題です。
上下し続けるおもりと,水面の高さの問題です。
水を吸収する素材でできた棒を水そうに沈める問題です。
水量変化の応用問題です。穴ではなくてポンプの設定なので,水が変わった動きをします。
2020年の西大和学園県外入試でも出題された,立体図形と角度の問題です。
立体図形と角度の問題の第2弾です。
立体図形における角度の問題の第3弾です。
立体における最短距離・角度・面積の比に関する問題です。
さいころ転がしに関する,誘�導が長めの問題です。
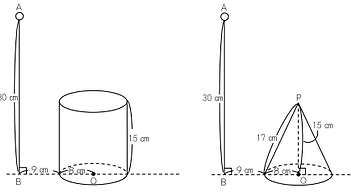
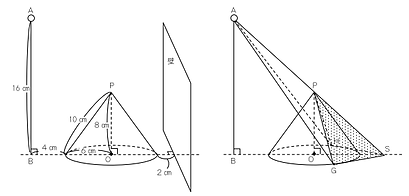
ひもの届く範囲の,やや変則的な問題です。
連なった四角すいを切断する問題です。
山脈の切断・1をあしらったグッズを販売しております。
三角すいを連ねた「山脈」を切断する問題です。
開成中平成10年の類題です。
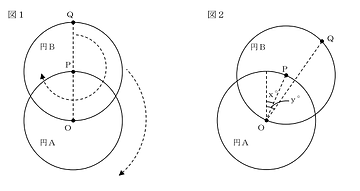
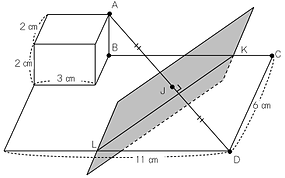
立体的な状況設定で,2点のそれぞれに近い部分に空間を分ける問題です。
立方体及び直方体について,いくつかの頂点の間で近い部分の範囲を考える問題です。
正四面体の各頂点からの近さ・遠さの範囲を考える問題です。
近さの範囲・正四面体をあしらったグッズを販売しております。
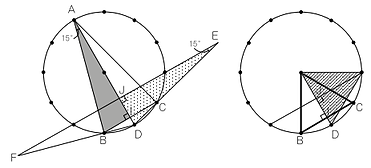
正八四面体の各頂点からの近さ・遠さの範囲を考える問題です。定規とコンパスを用いた作図の設問を伴っています。
正方形を回転させてできる立体に関する問題です。
三角すいを回転させたときの,複数の面の通過後の体積を求める問題です。
四角すいを回転させてできるいろいろな回転体の問題です。
ねじれたような形の立体について,辺や面の平行・垂直の関係から底面を探り当てる問題です。
三角すいの頂点の位置を色々と変えることに伴って,「底面」がどのように変化するのかを考える問題です。
三角すいの側面が通過してできる回転体は果たして円すいの側面の一部になるのか…という問題です。
ねじれた位置関係で回転する2点を結ぶ線分が通過する部分について考える問題です。円すいの側面にはなりません。
ねじれた点移動をあしらったグッズを販売しております。
四角すいを少しだけ回転させたときに,側面が通過する部分の体積を求める問題です。
ピタゴラス数を求めつつ,三角柱の回転について考える問題です。
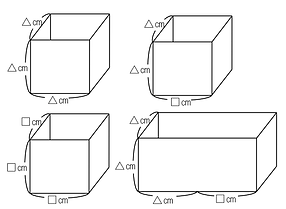
いわゆる踏み台型の立体についていろいろと考える問題です。
複合立体を変形させたときの体積の変化に関する問題です。
四角すいの辺上を往復する4点がいつの平面上に並ぶ時間を求める問題です。
三角すいを前後や左右に平行移動させる問題です。
立方体が四角すいの外周を自由に平行移動する問題です。
辺の長さがフィボナッチ数になる立方体をらせん状に並べてできる立体の表面積に関する問題です。